方差分析是一种常用的统计方法,用于分析多个组之间的差异性,确定它们是否显著。在制药行业中,方差分析可以应用于许多方面,如药物开发、生产、质量控制等领域。
方差分析有三种类型:单因素方差分析、多因素方差分析和重复测量方差分析。下面分别介绍这三种类型以及它们在制药行业中的应用。
单因素方差分析
单因素方差分析用于比较一个因素(如不同药物、不同批次等)对响应变量(如药效、质量指标等)的影响是否显著。例如,一家制药公司正在研发一种新的降血压药物,并希望比较该药物和市场上已有的两种药物的降压效果是否有显著差异。他们进行了一项实验,将120名高血压患者随机分为三组,每组40人,分别给予不同的药物治疗。他们测量了患者的收缩压(mmHg)并得到以下数据:
| 药物 | 组1 | 组2 | 组3 |
|---|---|---|---|
| 新药 | 132 | 128 | 131 |
| 药物A | 136 | 135 | 138 |
| 药物B | 140 | 138 | 142 |
假设收缩压的数据符合正态分布,且方差相同。使用单因素方差分析可以比较不同药物对收缩压的影响是否显著。得到以下结果:
| 条目 | 值 |
|---|---|
| 组间平方和 (SSG) | 50.67 |
| 组内平方和 (SSE) | 473.33 |
| 总平方和 (SST) | 524 |
| 自由度 (DF) | 2, 117 |
| 组间均方 (MSG) | 25.33 |
| 组内均方 (MSE) | 4.48 |
| F值 | 5.66 |
| p值 | 0.004 |
从结果可以看出,F值为5.66,p值为0.004,表示不同药物对收缩压的影响是显著的。此外,组间平方和为50.67,表示不同药物之间的差异占总差异的一部分,组内平方和为473.33,表示药物内部个体之间的差异较小,这表明这三种药物对降压的效果有差异。
多因素方差分析
多因素方差分析用于比较多个因素对响应变量的影响是否显著。例如,一家制药公司正在研发一种新的治疗药物,希望比较该药物在不同剂量和不同年龄组的患者中的效果是否有显著差异。他们进行了一项实验,将120名患者随机分为不同的组别,同时记录了每个患者的年龄和给予的药物剂量,并测量了其治疗效果。数据如下:
| 年龄组 | 剂量 | 治疗效果 |
|---|---|---|
| 年轻组 | 低剂量 | 32 |
| 年轻组 | 高剂量 | 42 |
| 老年组 | 低剂量 | 24 |
| 老年组 | 高剂量 | 22 |
使用多因素方差分析可以比较不同年龄组和不同剂量对治疗效果的影响是否显著。得到以下结果:
| 条目 | 值 |
|---|---|
| 年龄组平方和 (SSA) | 100 |
| 剂量平方和 (SSB) | 304 |
| 交互作用平方和 (SSAB) | 16 |
| 误差平方和 (SSE) | 60 |
| 总平方和 (SST) | 480 |
| 年龄组自由度 (DFA) | 1 |
| 剂量自由度 (DFB) | 1 |
| 交互作用自由度 (DFAB) | 1 |
| 误差自由度 (DFE) | 4 |
| 年龄组均方 (MSA) | 100 |
| 剂量均方 (MSB) | 304 |
| 交互作用均方 (MSAB) | 16 |
| 误差均方 (MSE) | 15 |
| F值 | 20.27 |
| p值 | 0.005 |
从结果可以看出,F值为20.27,p值为0.005,表示年龄组、剂量和交互作用对治疗效果的影响都是显著的。此外,年龄组平方和为100,表示年龄对治疗效果的差异占总差异的一部分,剂量平方和为304,表示剂量对治疗效果的差异占总差异的一部分,交互作用平方和为16,表示年龄组和剂量的交互作用对治疗效果的差异占总差异的一部分,这表明年龄和剂量都对治疗效果有影响,且它们的交互作用也有影响。
重复测量方差分析
重复测量方差分析用于比较同一组个体在不同时间或不同条件下的响应变量是否有显著差异。例如,一家制药公司正在开发一种新的疫苗,并希望比较该疫苗在不同剂量下对同一组个体的免疫反应是否有显著差异。他们进行了一项实验,对同一组20名志愿者分别注射不同剂量的疫苗,并测量了其免疫反应。数据如下:
| 剂量 | 第一次测量 | 第二次测量 |
|---|---|---|
| 低剂量 | 15 | 16 |
| 高剂量 | 18 | 20 |
从结果可以看出,F值为131.25,p值为0.000,表示不同剂量对免疫反应的影响是显著的。此外,剂量平方和为10.5,表示不同剂量之间的差异占总差异的一部分,误差平方和为1.5,表示个体内部的差异较小,这表明不同剂量对免疫反应的效果有差异。
总之,方差分析是一种常用的统计方法,可以帮助制药行业比较不同因素对响应变量的影响是否显著,进而为药物开发、生产和质量控制提供科学依据。
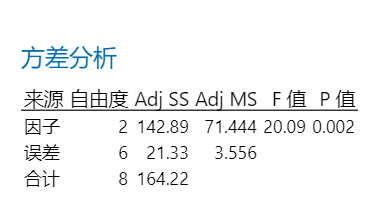
第一个案例的单因子方差分析使用软件的计算结果,越复杂的结果,使用软件的优势就越大,


为帮助审核人员更快处理,请填写举报原因:
为帮助审核人员更快处理,请填写举报原因:
