假设检验是一种统计方法，用于检验一个关于总体参数的假设是否成立。在假设检验中，我们通常有两个相互对立的假设：零假设（H0）和备选假设（H1）。零假设通常表示没有差异或者没有效果，而备选假设表示存在差异或者有某种效果。我们通过分析数据，计算一个统计量（如t值或z值）和相应的p值（概率值），然后根据p值来判断是否拒绝零假设。
让我们通过几个制药行业的例子来更好地理解假设检验：
新药疗效评估： 在这个例子中，我们要检验一种新药是否比现有的治疗方法更有效。零假设是新药和现有药物在疗效上没有差异，而备选假设是新药的疗效更好。通过收集两组患者（一组接受新药治疗，另一组接受现有药物治疗）的数据，我们进行统计分析。如果计算出的p值低于我们设定的显著性水平（通常为0.05），我们就拒绝零假设，认为新药疗效更好。
药物副作用研究： 在这个例子中，我们要研究一种药物是否会导致某种副作用。零假设是药物不会导致该副作用，备选假设是药物会导致副作用。我们会收集使用该药物的患者数据，并记录副作用的发生情况。根据统计分析结果，如果p值低于显著性水平（如0.05），我们就拒绝零假设，认为药物可能导致该副作用。
药物剂量和疗效关系研究： 在这个例子中，我们想要研究药物剂量是否影响其疗效。零假设是药物剂量与疗效无关，备选假设是药物剂量与疗效相关。我们可以收集不同剂量药物治疗患者的数据，然后进行统计分析。如果p值低于显著性水平（如0.05），我们就拒绝零假设，认为药物剂量和疗效之间存在关系。 总之，假设检验是一种有力的统计工具，可以帮助制药行业在研发、监管和临床中有重大意义。 单样本t检验是一种假设检验方法，用于比较来自总体的一个样本的均值是否显著地与某个已知值或理论值不同。在制药工艺方面，我们可以通过单样本t检验来检验某种药物制剂的纯度是否达到了预期的标准。
假设检验常用工具——单样本T检验
假设我们有一个新的生产工艺，目标是生产纯度为98%的药物制剂。为了检验生产出的药物制剂纯度是否满足预期，我们从生产批次中随机抽取了10个样本，测量它们的纯度。以下是纯度数据（百分比）：
96.5, 98.3, 97.9, 98.7, 97.1, 98.2, 99.0, 97.6, 98.5, 98.1
在这个例子中，我们进行单样本t检验。零假设（H0）是生产出的药物制剂的纯度达到了98%，即总体均值为98%。备选假设（H1）是生产出的药物制剂的纯度不等于98%，即总体均值不等于98%。
我们首先计算样本均值（x̄）和样本标准差（s）。使用上述数据，我们得到：
x̄ = (96.5 + 98.3 + 97.9 + 98.7 + 97.1 + 98.2 + 99.0 + 97.6 + 98.5 + 98.1) / 10 ≈ 98.0%
s ≈ 0.93% 接下来，我们计算t值：t = (x̄ - μ) / (s / √n) = (98.0 - 98) / (0.93 / √10) ≈ 0
其中，μ是总体均值（理论值，即98%），n是样本数量（10个）。计算出t值后，我们可以查找相应的p值。由于我们的备选假设是不等于，所以我们进行双侧检验。在这种情况下，p值接近1，远大于显著性水平（如0.05），因此我们不能拒绝零假设。这意味着，我们没有足够证据表明生产出的药物制剂纯度不等于98%。
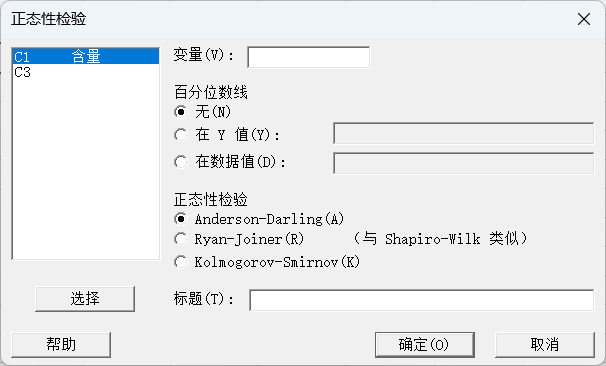
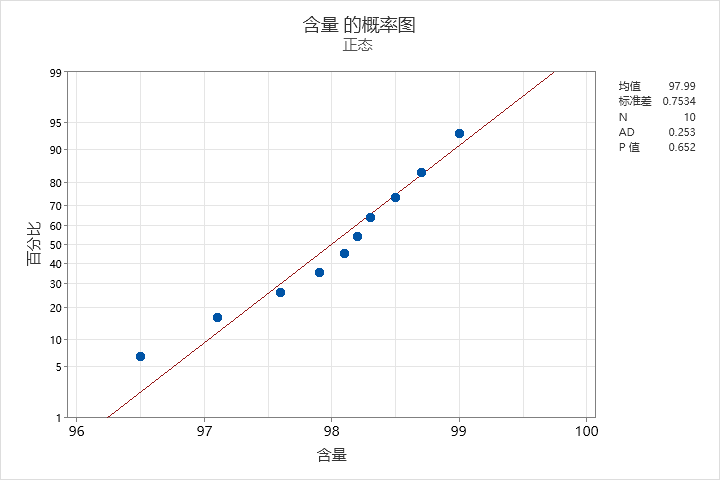
需要注意的是，单样本t检验依赖于数据满足正态分布假设。在实际应用中，我们可能需要对数据进行正态性检验，以确保检验的有效性。 手工计算还是繁琐，使用统计软件就方便多了： 首先进行正态性检验：
然后进行单样本T检验： 
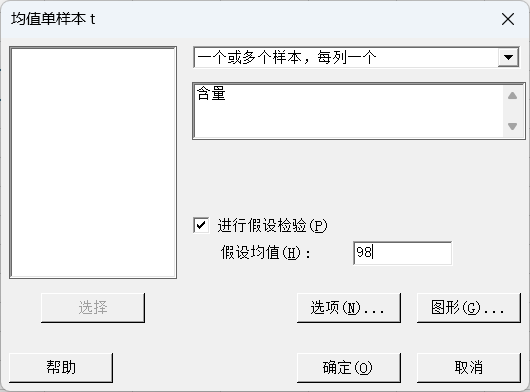
可以得出手工计算同样的结论（我真的不是给统计软件做广告)
为帮助审核人员更快处理，请填写举报原因：
为帮助审核人员更快处理，请填写举报原因：