声明：1）本文系原创，转载须经作者同意并包括原文链接 2）【】中数字是文末参考文献号 3）不妥及争议之处欢迎留言探讨

一、背景及问题

取样（sampling）是药品生产工作不可缺少的一部分。无论物料还是成品都是通过取样、样品检验/检查，来决定是否被接受或放行。取样一定有一个取样方法（sampling procedure）和取样计划（sampling plan），包括如何获取样品，取多少，样品如何检查/检验，结果如何判断等。

那么问题来了：如何判断一个取样计划是否合理有效？又如何设置有效的取样计划？当取样计划已确定，您又有多大把握某批正常产出的产品会通过既定的取样计划呢？或者说下个批次通过该取样计划的概率是什么？本文将就这些问题进行探讨。

为了方便阅读，本文将以最简单的计数型取样方法，即检查取出的每个样品是否合格，来阐述取样计划的概念和其相应的抽验操作特征曲线（Operating Characteristic Curve，OC-Curve）。

二、有关取样的一些关键概念

取样是药品生产控制策略的一个重要组成部分。与其相关的有三个非常重要的概念，分别是取样计划、取样方略和取样系统。平常工作中使用最多的是取样计划，但质量工作者应当区分取样计划、取样方略和取样系统，这三个词不应混用。

1. 取样计划（sampling plan）：是指取样量（n）和与之相对应的批次可接受值（c）的组合【1】。取样计划有多种，常见的有单次取样计划（Single sampling plan）、双次取样计划（double sampling plan）和多次取样计划(multiple sampling plan),以及顺序取样计划（Sequential sampling plan）等【2】。由于篇幅的原因，这里不做详细的解释。注意：取样计划不包括如何从批次中获取样品【1】，这应该被称为取样方法（sampling procedure）。

2. 取样方略（sampling scheme）是指一组取样计划，在这些取样计划之间设有一些原则允许从一个取样计划转换为另一个取样计划【2】。

3. 取样体系（sampling system）: 是指由不同的取样计划和取样方略所组成的一个系统，其中包括取样计划和取样方略之间的切换的原则【2】。

以ISO 2859-1标准为例，取样量n=34和可接受值c=3组成一个取样计划。字母J所对应的AQL 为1.0的所有取样计划形成了一个取样方略，而整个ISO 2859-1标准则是一个取样系统【2】。

三、抽验操作特征曲线（Operating Characteristic Curve）的概念

假设有100副扑克牌，每副扑克牌都有一张没印上任何花色的不合格白板张，随机分布在54张牌（算上大小王）中。对这100副牌的每副牌都进行100%检查。因为白板张与其他牌的区别非常明显，且检查得又非常认真，不会造成混淆。那么，这100副牌都会被判定为不合格。

一副牌有54张，一张白板所占的比例是1/54，可以将这个1/54称为“批次不合格率”，而这个取样计划(sampling plan)则可被称为100%检查（screening）。此方法可以推论，一副牌中有多余一张的白板，在进行100%检查后也会被判定为不合格，即合格率为0。当然如果一副牌中无白板张，其合格率则是100%。此时，将批次中的不合格牌张数和合格率做图，就可得到如下图的曲线：有0张不合格牌张时，100%合格，而有1张及以上的白板张时，合格率则为0。这种曲线被称为“抽验操作特征曲线（Operating Characteristic Curve，OC-Curve）”。

很显然，这是理想状态，实际工作中很少有这种情况，即便是100%检查也不可能100%有效。那么，继续上面的实验，假设还是这100副牌，每副牌都有1张随机混合在牌中的不合格白板张，换一个取样计划，每副抽取一张牌，看看是不是白板，作为判断这副牌是否合格的依据。这个取样计划可被表示为“n=1，c=0”。概率理论表明，如果一副牌中只有一张白板，一次取一张，抽到白板的概率是1/54。即按这个取样计划，这副牌被抽验不合格的概率为1/54。换句话说，这100副牌中会有100X(1/54)=1.9约两副牌会被该取样计划判定为不合格，而另外约98副牌会被判定为合格。这就是这个取样计划对质量的影响效果。

继续上面的取样计划n=1，c=0，改变牌中不合格的张数。假设每盒牌中有2张白板，每次抽取一张，抽到一张白板的概率则是2/54，也就是说一副牌只有2/54的机会被判定为不合格，那么其抽验合格概率则为（1-2/54=）52/54。如果每盒牌中有3张白板，抽取一张为白板的概率是3/54，它的抽验合格概率则是51/54。以此类推，当一盒牌中有53张是白板时，抽取一张牌是白板的几率为53/54，其抽验合格概率则为1/54。如果所有的54张牌都是白板，当然每次抽出来的都是白板，它的抽验合格概率则为0。当然，如果一副牌中所有牌张都是正确的，抽出任一张牌肯定不会是白板，这副牌的抽验合格概率会是100%。将这样的数据做图，得出如下的抽验操作特征曲线(OC-Curve)。

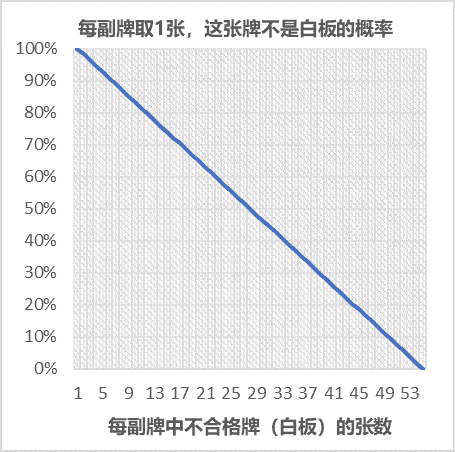
当然，这是最简单的取样计划，实际工作很少有这样的取样计划,因为取样量很少有n=1的情况。例如ISO 2859-1中取样量最小的是2【1】。

继续同样的实验，但取样量变为2张牌，没有白板为合格。这个取样计划可表示为n=2，c=0。这时计算每副牌的合格概率稍微复杂一些，最好借助计算机来进行。如，可采用Excel的Hypgeom.dist()函数来计算取2张牌中0张白板的概率，也就是该取样计划的抽验合格概率。下表列出了牌中的不合格张数与Excel的Hypgeom.dist()函数计算出来的相应的可接受概率（至于为什么要采用这个函数，不属于本文要讨论的内容，感兴趣的读者可以留言探讨）。

将这个数据做出曲线如下图。

如果再修改一下上面的取样计划，还是取两张n=2，可接受的白板数为1，即c=1。即取出的两张牌中，如果有一张是白板，这副牌仍会被认为是合格的。此时，抽验合格概率的计算就更复杂一些。同样可采用Excel中的Hypgeom.dist()函数来计算取2张牌中出现1张和0张白板的总概率，即抽验合格概率，计算出来的结果如下表。

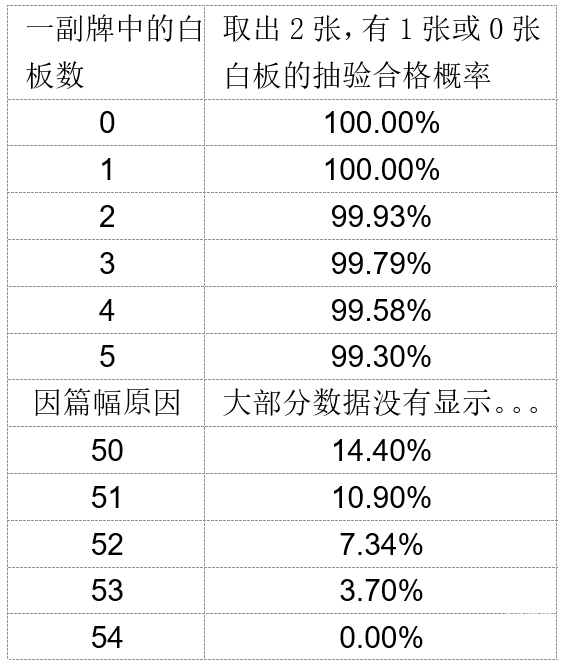
将这个数据做出曲线如下图。

将这两条曲线放在一张图上的效果是这样子的。

比较上图中这两个抽验操作特征曲线，可以看出，同样的不合格率的批次，通过蓝线取样计划（n=2,c=1）的概率大于通过橘黄线取样计划（n=2,c=0）。

上述实验还说明，当给定一个取样计划（如n=2,c=1），一副牌中的任意一个数目的不合格张数（如5张）都可能会被这个取样计划判定为合格或者不合格，只是概率不同。这与检验本身无关，与质量标准（specifications）也无关。这完全是由取样本身的概率决定的。

将上面的实验的扑克牌换成药片、胶囊、西林瓶、软膏剂，比如54片药中，取出两片，检查是否有外观缺陷，道理是完全一样的。图示OC-curve的生产商风险和消费者风险是也是一样的。

四、解读抽验操作特征曲线

所有抽验操作特征曲线的构成都是一样的，其横轴是批次的不合格率或百分率，纵轴是批次通过取样计划的概率，总是从0~1，所显示的通常是一条曲线，即OC-curve，表示批次的不合格率所对应的被取样计划判定为合格的概率。从横轴的任何一点画一条直线与曲线相交，再画一条横线到纵轴所对应的值，就是此不合格率通过该取样计划的概率，即批次可接受概率。上图两条曲线上各标示出两个点，蓝色曲线所代表的取样计划(n=2,c=1)显示，当一副牌中有12张不合格张时，它所对应的可接受概率大约是96%（绿点）；而当一副牌中有52张不合格牌张时，其可接受概率仍然有10%（红点）。而橘黄色曲线所代表的取样计划(n=2,c=0)要达到同样的可接受概率，不合格牌张的数分别是1和12。这就是不同取样计划的区别。

根据上述对OC-Curve的讨论，可以结论，除非批次的不合格率为0或100%，任何水平的批次不合格率在实施一个取样计划时，都存在一个被接受的概率（p1）和被拒的概率(p2)，其关系是p1+p2=1。这是抽验操作特征曲线最重要的理论基础，也是其应用的关键基础。

通俗地说，只要对某个批次按照某个取样计划进行取样检验，这个批次就必然面临被接受或被拒的风险（概率）。这是由取样操作本身的性质决定的。这个结论隐含着两个重大假设，一是检验本身不会影响对结果的判断，二是所获取的样品是随机的或完全能够代表批次本身。

大约100年前，质量管理大师们就对这种被接受或被拒的风险（概率）进行了定义。这种由于取样计划本身将一个“好的”批次判定为不合格的概率被称为生产商风险（producer risk），也称为α风险；而一个取样计划将“不好”的批次判定为合格的概率，被称为消费者风险（consumer risk），也称为β风险。

以ISO 2859-1中的一个取样计划: 字母H, AQL=1.0, n=50，c=1，为例，这个取样计划的OC-curve如下图。

上图显示，当批次的不合格率为0.65%时，其可接受概率约为95%，即会有5%的概率被拒批，也就是生产商的风险为α=5%，质量管理大师们将这种大多数时候都能够通过某个取样计划的批次质量水平即不合格率水平称为生产商质量水平（Producer Quality Level-PQL）。

上图中的批次不合格率约为7.6%时，批次会有约10%的通过率或者可接受概率，即消费者风险β=10%。质量管理大师们将这种大多数时候会被取样计划拒批的批次质量水平称为消费者质量水平（Consumer Quality Level-CQL）【3】。

生产商质量水平(PQL)往往会混淆于“可接受质量水平（Acceptance Quality Level亦或Acceptance Quality Limit-AQL）”【1】【2】【3】。AQL这个词主要是用于抽样检验（acceptance sampling）。ISO 2859-1将AQL定义为“将一系列批次提交抽样检验时，能容忍的最低工艺平均水平”。工艺平均水平（process average）则是指“批次不合格百分率或每100个产品中的不合格数量”【1】。 所谓“能容忍的最低工艺平均水平”则是指批次有较大的概率通过该取样计划。通常会把这个较大的概率定为95%【3】，也有定99%，或90%以上的其他数值【2】。上面例子中的批次不合格率0.65%就是取样计划（n=50，c=1）的AQL。一个取样计划的选择应使得生产商的质量风险等于或者小于AQL【2】。

与AQL相对应的一个词是批次容忍不合格率（Lot Tolerance Percent Defective-LDPT）,指批次的某个质量水平（即不合格率），它会使得批次通过取样计划的概率为10%。即具有这种质量水平的批次只有10%的机会被取样计划判定为合格【2】【3】。

容易与LTPD混淆的一个词是“限定质量(Limiting Quality-LQ)”或“被拒质量水平(Rejectable Quality Level-RQL)”【2】。与AQL不同，LQ是指一个孤立批次的质量水平（不合格率），在此质量水平下对批次实施取样抽验，仅有低概率会接受这个批次。可见，与AQL一样，LQ也代表批次不同的质量水平，可以是任何值，只是这些质量水平通过取样计划的概率较低。 当LQ所对应的批次通过概率为10% 时，这个LQ值就是LTPD。可以说，LTPD是LQ的一个特定质量水平点【2】。 LQ值可以被用来对孤立批次的取样检验建立取样计划索引，如ISO 2859-2【2】。

五、抽验操作特征曲线的应用

任何一个取样计划都对应着一条抽验操作特征曲线。根据这条曲线就可知道不同不合格率的批次通过该取样计划的概率。它可以用来回答本文开篇提出的问题。如果已知某个工艺所生产批次的不合格率的平均值（可以通过历史数据得出），就可查询抽验操作特征曲线得出通过这个取样计划的概率，即有多大的把握这个批次会被该取样计划接受，即判定为合格。

抽验操作特征曲线的另一重要用途是根据客户对质量的要求，生产商可以指定相应的取样计划。抽验操作特征曲线可证明这个取样计划能够达到用户的质量要求。欲设计适合的取样计划，需要四个数据：AQL、α、LTPD和β。

那么，什么是一个好的取样计划？选择取样计划需要综合考虑、平衡生产商风险和消费者风险。除了有法律法规规定的取样要求外，选择取样计划是一个经济问题，因为不同的取样计划，也就是不同的取样量会达到相同的对消费者风险的保护。这需要了解取样量和可接受值对取样计划的OC-Curve的影响。
如下图所示，如果保持可接受值不变，取样量越大同样的批次不合格率所对应的可接受概率越低。

如上图所示,假如可接受标准为不大于0.30%，而批次的平均不合格率0.05%±0.05。那么采用n=100，c=1的取样计划会造成太多没有必要的拒批亦或太多的OOS调查，可又找不到任何OOS的原因。这样的取样计划会累死全公司的员工，却得不到任何保护消费者的好处。

反之，为了增加信心，在选取工艺验证的取样计划时，会加大取样量，有意在工艺验证时降低工艺平均质量水平通过取样计划之概率，从而确保在商业化产生中由于取样量减少，则会增加通过取样计划的概率，即增加信心。

如果变换上面的取样计划，保持取样量不变，n=20, 但变换可接受值从0~3。这会形成下图的四条OC-curve。可见c值越小，同样不合格率的批次被取样计划接受的概率越低。

上图的曲线还告诉我们，c=0时，曲线会迅速下降，也就是说随着批次中不合格率的增加，可接受概率会急剧减少。因此有的时候采用c=0的取样计划并非最佳的方案。

那么是不是应该随着样品量的增加，可接受值也应增加呢？下图是一个保持可接受值是样品量的1/10的一组OC-curve。

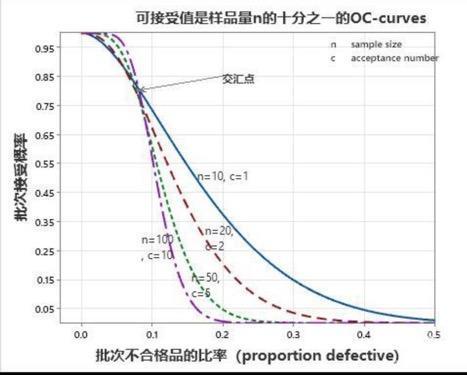
可以看出，这些曲线在大约80%的通过率的地方相交。这表明在批次不合格率大约在0.08%时这些取样计划的通过概率是一样的。

上面这些曲线都表明，确保批次能大概率通过取样计划的重要手段是降低批次平均不合格率水平，使得工艺平均不合格率远低于AQL，这样则可确保批次有更高的概率通过取样计划。

六、讨论与总结

无论取样计划（sampling plan）判定批次合格与否，取样检验（acceptance sampling）本身不会改变批次的质量水平（percent of defectives）【3】。取样计划主要由取样量(n)和可接受值(c)组成。每个取样计划都对应一条“抽验操作特征曲线OC-curve”，显示批次中的不合格率所对应的批次通过取样计划概率。除非批次质量水平是0或者100%，实施取样检验都存在被取样计划接受和被拒的风险。取样计划将一个本应合格的批次判定为不合格的概率被称为生产商风险，而将一个本来不合格的批次判定为合格的概率称为消费者风险。取样计划的选择必须考虑和平衡这两方面的风险。这种风险完全是由于取样概率所决定的，与检验方法的准确与否以及客户可接受标准没有关系。

七、参考文献：

【1】ISO 2859-1 Sampling Procedure for inspection by attributes – Part 1， 1999
【2】Joseph M. Juran: Juran’s Quality Handbook, 5th Edition, McGraw-Hill, 1998
【3】E. G. Schilling & D. V. Neubauer, Acceptance Sampling, 3rd, Taylors & Francis Group, 2017